Your system is not supporting JavaScript.

Multiple Dimensions

Home Page Math Portal Numbers & Operations Algebra Geometry Trigonometry Pre-Calculus Calculus Multiple Dimensions Set Theory Statistics
79865 45962 20137 2106 3923 87 1837 39961 2667 1433 2098

Math Involved: Lines Planes Distances Mid-Points Angles Areas
Tesseract, Cube, Square Image Video Coordinates Characteristics
Tetrahedron, Triangle Images Coordinates Characteristics Useful Facts
Other 3d Platonic Solids: Octahedron (8 sided) Dodecahedron (12 sided) Icosohedron (20 sided)
Sphere, Circle

http://www.coolmath4kids.com/polyhedra/index.html

Math Involved

Lines

The relationship between any two dimensional values of a line in multiple dimensions is linear, so the equation of a four dimensional line can be defined by this set of equations (Certain combinations of three of the equations define the line, such as the upper three. The other equations are extra equations that are also true statements):
x=m1y+b1
y=m2x+b2
x=m3z+b3
y=m4z+b4
z=m5x+b5
z=m6y+b6
x=m7a+b7
y=m8a+b8
z=m9a+b9
a=m10x+b10
a=m11y+b11
a=m12z+b12

Another form of an equation of a line in multiple dimensions is:
[x,y,z,a]=x*[1,m1,m2,m3]+[0,b1,b2,b3]
which can be simplified to:
[y,z,a]=x*[m1,m2,m3]+[b1,b2,b3]

Planes

The equation of a plane in three dimensions is:
z=m*x+n*y+b
whereas x, y, and z are variables and m, n, and b are constants.

The equation of a plane in multiple dimensions is:
[x,y,z,a]=x*[1,0,m1,m2]+y*[0,1,n1,n2]+[0,0,b1,b2]
which can be simplified to:
[z,a]=x*[m1,m2]+y*[n1,n2]+[b1,b2]

Cubicals

The equation of a cubical in four dimensions is:
a=m*x+n*y+p*z+b
whereas x, y, z, and 'a' are variables and m, n, p, and b are constants.

The equation of a cubical in multiple dimensions is:
[x,y,z,a,c]=x*[1,0,0,m1,m2]+y*[0,1,0,n1,n2]+z*[0,0,1,p1,p2]+[0,0,0,b1,b2]
which can be simplified to:
[a,c]=x*[m1,m2]+y*[n1,n2]+z*[p1,p2]+[b1,b2]

Distances

Coordinates are listed in the form of (x,y,z,a,b,c,d,...) depending on how many dimensions are used. (3,4,0,0) is equivalent to (3,4). (5,0) is equivalent to (5). To find the distance between two points that are given coordinates, let d=distance and use the equation d = √((x1-x2)2+(y1-y2)2+(z1-z2)2+(a1-a2)2+...).

Proof of the distance formula for three dimensions:
Let there be the two points J(a,b,c) and K(d,e,f).
'd' is defined the distance from J to K to be solved.
K-J=(0,0,0)-(K-J)=(x,y,z); The distance from K to J is the same as the distance from (0,0,0) to (K-J).
Let 'p' equal the distance from (0,0,0) to (x,y,0)
p=√(x^2+y^2)
The angle from (0,0,0) to (x,y,0) to (x,y,z) is 90 degrees with its hypotenuse the length 'd'.
d=√(p^2+z^2)
substitute: d=√((√(x^2+y^2))^2+z^2)
symplify: d=√(x^2+y^2+z^2)
substitute: d=√((a-d)^2+(b-e)^2+(c-f)^2)

dist(A,B)=sqrt(sum((A-B)^2))

Mid-Points, Third-Points, and Twice-Points, etc.

To find the coordinate half or 1/3 or 5 times or v times the distance from (x1,y1,z1,a1) to (x2,y2,z2,a2) use the formulas:
x3 = (x2-x1)*v+x1
y3 = (y2-y1)*v+y1
z3 = (z2-z1)*v+z1
a3 = (a2-a1)*v+a1
or use the combined single formula:
{x3,y3,z3,a3} = ({x2,y2,z2,a2}-{x1,y1,z1,a1})*v+{x1,y1,z1,a1}

mid(A,B)=(A+B)/2
vMid(A,B,v)=(B-A)*v+A

Angles

dist(P,R)=PR

To find the shortest angle between two segments which are connected by one point (if you know their coordinates), use the distance formula to find the distances between each of the three points and then use the law of cosines to find the angle. For example, the angle from P(x1,y1,z1,a1) to the corner Q(x2,y2,z2,a2) to R(x3,y3,z3,a3) can be calculated by the formula cos-1((PR2-QP2-QR2)/(-2*QP*QR)). After substituting in the exact distances and symplifying, the formula becomes cos-1(((x1-x3)2+(y1-y3)2+(z1-z3)2+(a1-a3)2)-(x1-x2)2-(y1-y2)2-(z1-z2)2-(a1-a2)2)-(x2-x3)2-(y2-y3)2-(z2-z3)2-(a2-a3)2))/(-2*√(((x1-x2)2+(y1-y2)2+(z1-z2)2+(a1-a2)2)*((x2-x3)2+(y2-y3)2+(z2-z3)2+(a2-a3)2)))). Note that the range of the output (the angle) is [0,180] while not including (180,360).

angle(P,Q,R)=cos-1(sum((P-R)^2-(P-Q)^2-(Q-R)^2)/(-2*sqrt(sum((P-Q)^2+(Q-R)^2))))

Area of triangle

Given points

A(x1,y1,z1) B(x2,y2,z2) C(x3,y3,z3)
These are only true if the liine from point C to the point inbetween A and B is tangent to the line from A to B:
dist(A,B)*dist(mid(A,B),C)/2=area
sqrt(sum((A-B)^2)*sum(((A+B)/2-C)^2))/2=area
True for any triangle:
When the derivative of the distance between the point and the base line is 0; the minimax of the distance between the point and the base line.

Given 3 lengths

a,b,c
area=sqrt(2*((a*b)^2+(a*c)^2+(b*c)^2)-a^4-b^4-c^4)/4=c*b*sqrt(1-((b^2+c^2-a^2)/(2*b*c))^2)/2

Given 1 angle and 2 lengths

θ=C,a,b
sin(θ)*a*b/2=area

Given 2 angles and 1 length

θ1=A,θ2=B,c
c^2*sin(θ2)*sin(θ1)/(2*sin(θ1+θ2))=area

Comprehensive Overview

Number of points that make hedrons in multiple dimensions
0 1 2 3 4
0 1
1 2
2 3 4 5 6 7
3 4 6 8 12 20
4 5 16
Number of segments (lines) that make hedrons in multiple dimensions
0 1 2 3 4
0 0
1 1
2 3 4 5 6 7
3
4
Number of faces (planes or areas) that make hedrons in multiple dimensions
0 1 2 3 4
0 0
1 0
2 1 1 1 1 1
3 4 6 8 12 20
4 5 16
Number of volumes that make hedrons in multiple dimensions
0 1 2 3 4
0 0
1 0
2 0 0 0 0 0
3 1 1 1 1 1
4 5 8
Number of d-1 that make hedrons in multiple dimensions
0 1 2 3 4 5
0
1 2
2 3 4 5 6 7 8
3 4 6 8 12 20
4 5 8 16 24 120 600
http://www.webdragon.com/geometry/4dtetri.html
http://www.webdragon.com/geometry/shapes.html
Top of Page

Tesseract

Image

A 3d image of a 4d tesseract, constructed with toothpicks.
tesseract

Video

This video shows a tesseract rotating through the fourth dimention. A tesseract is a four dimensional cube.

Coordinates

Four dimensions of space means that there are four axis. Coordinates are written in the form (x,y,z,a). Another name for a tesseract is an octaholohedron meaning: 8 three-dimensional sides (http://www.webdragon.com/geometry/4docta.html). The points, lines and areas of a tesseract are:
label
x
y
z
a
A
0
0
0
0
B
1
0
0
0
C
0
1
0
0
D
1
1
0
0
E
0
0
1
0
F
1
0
1
0
G
0
1
1
0
H
1
1
1
0
I
0
0
0
1
J
1
0
0
1
K
0
1
0
1
L
1
1
0
1
M
0
0
1
1
N
1
0
1
1
O
0
1
1
1
P
1
1
1
1
Label
Segment
1
AB
2
AC
3
CD
4
BD
5
EF
6
EG
7
FH
8
GH
9
AE
10
BF
11
CG
12
DH
Label
Segment
13
IJ
14
IK
15
JL
16
KL
17
MN
18
MO
19
NP
20
OP
21
IM
22
JN
23
KO
24
LP
Label
Segment
25
AI
26
BJ
27
CK
28
DL
29
EM
30
FN
31
GO
32
HP
Label
Area
1
ABDC
2
EFHG
3
ABFE
4
CDHG
5
ACGE
6
BDHF
7
IJLK
8
MNPO
9
KLPO
10
IJNM
11
IKOM
12
JLPN
Label
Area
13
ABIJ
14
CDLK
15
ACKI
16
BDLJ
17
EFNM
18
GHPO
19
EGOM
20
FHPN
21
AEMI
22
CGOK
23
BFNJ
24
DHPL

As you can see the coordinates look just like binary code.

Characteristics

This table shows the number of lines, areas, volumes, four dimensional volumes, ... in the point-to-line-to-square-to-cube-to-tesseract pattern.
y
Dimensions
-1
0
1
2
3
4
5
6
7
x
-1
0
0
0
0
0
0
0
0
0
0
0
Points
1/2
1
2
4
8
16
32
64
128
2x
1
Segments
-1/4
0
1
4
12
32
80
192
448
x*2x/(1!*21)
2
Areas
1/8
0
0
1
6
24
80
240
672
(x-1)*x*2x/(2!*22)
3
Volumes
-1/16
0
0
0
1
8
40
160
560
(x-2)*(x-1)*x*2x/(3!*23)
4
4D volumes
1/32
0
0
0
0
1
10
60
280
(x-3)*(x-2)*(x-1)*x*2x/(4!*24)
5
5D volumes
-1/64
0
0
0
0
0
1
12
84
(x-4)*(x-3)*(x-2)*(x-1)*x*2x/(5!*25)
6
6D volumes
1/128
0
0
0
0
0
0
1
14
(x-5)*(x-4)*(x-3)*(x-2)*(x-1)*x*2x/(6!*26)
7
7D volumes
-1/256
0
0
0
0
0
0
0
1
(x-6)*(x-5)*(x-4)*(x-3)*(x-2)*(x-1)*x*2x/(7!*27)

Formula

This formula is used to calculate each of the equations in the table: ∑(2t-1*fv(x-t),t=1,x)→fv+1(x); f0(x)=2x
This formula is used to find the value of any cell if given its x and y coordinates in the table: ∏(x-t,t=0,y)*2x/(y!*2y)
Another pattern of the data is:
a
b
a+2b

Top of Page

Tetrahedron

Images

=edgelength2*sqrt(3)/4
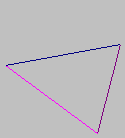
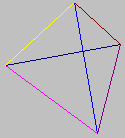
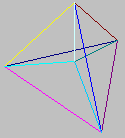
images of tetrahedrons of different dimensions
0d1d2d3d4d
1 length=1*height/1=height area=baselength*height/2 volume=basearea*height/3 4d_volume=basevolume*height/4
1 length=edgelength area=edgelength2*sqrt(3)/22 volume=edgelength3*sqrt(18)/(22*32) =edgelength3*sqrt(2)/12 4d_volume=edgelength4*sqrt(180)/(22*32*42) =edgelength4*sqrt(5)/96
tetrahedron 4d

Coordinates

Every point in a tetrahedron are connected to all the other points of the tetrahedron. All the lengths between any two points in a tetrahedron are the same length. The shortest angle between any two lines is 60 degrees. There is always one more point than the number of dimensions used in a tetrahedron; For example, a three dimensional tetrahedron has four points. The coordinates for a six dimensional tetrahedron are:
# of dimensions
x
y
z
a
b
c
0
0
0
0
0
0
0
1
√(1)/1
0
0
0
0
0
2
(√(1)/1)/2
√(3)/2
0
0
0
0
3
(√(1)/1)/2
(√(3)/2)/3
√(6)/3
0
0
0
4
(√(1)/1)/2
(√(3)/2)/3
(√(6)/3)/4
√(10)/4
0
0
5
(√(1)/1)/2
(√(3)/2)/3
(√(6)/3)/4
(√(10)/4)/5
√(15)/5
0
6
(√(1)/1)/2
(√(3)/2)/3
(√(6)/3)/4
(√(10)/4)/5
(√(15)/5)/6
√(21)/6
This shows a simplified exact form:
# of dimensions
x
y
z
a
b
c
0
0
0
0
0
0
0
1
1
0
0
0
0
0
2
1/2
√(3)/2
0
0
0
0
3
1/2
√(3)/6
√(6)/3
0
0
0
4
1/2
√(3)/6
√(6)/12
√(10)/4
0
0
5
1/2
√(3)/6
√(6)/12
√(10)/20
√(15)/5
0
6
1/2
√(3)/6
√(6)/12
√(10)/20
√(15)/30
√(21)/6

There is a pattern with the gold shaded numbers. If the number of dimensions used is labled "x", and the new coordinate value is labled "y", then √(x(x+1)/2)/(x)=y. As x approaches infinity, y approaches √(2)/2. You can see how the numbers below the golden shaded numbers are calculated. They are the same as the gold shaded number above them, but divided by (1 + its dimensional coordinate). They approach 0 as the number of dimensions approach infinity. The approximate points, rounded to the nearest ten thousandth, for a six dimensional tetrahedron are:
# of dimensions
x
y
z
a
b
c
0
0
0
0
0
0
0
1
1
0
0
0
0
0
2
0.5
0.8660
0
0
0
0
3
0.5
0.2887
0.8165
0
0
0
4
0.5
0.2887
0.2041
0.7906
0
0
5
0.5
0.2887
0.2041
0.1581
0.7746
0
6
0.5
0.2887
0.2041
0.1581
0.1291
0.7638

Characteristics

This table shows the number of lines, areas, volumes, four dimensional volumes, ... in the point-to-line-to-triangle-to-tetrahedron pattern.
y
Dimensions
-1
0
1
2
3
4
5
6
7
x
-1
no existance?
1
1
1
1
1
1
1
1
1
1
0
Points
0
1
2
3
4
5
6
7
8
x+1
1
Lines
0
0
1
3
6
10
15
21
28
x*(x+1)/2!
2
Areas
0
0
0
1
4
10
20
35
56
(x-1)*x*(x+1)/3!
3
Volumes
0
0
0
0
1
5
15
35
70
(x-2)*(x-1)*x*(x+1)/4!
4
4D volumes
0
0
0
0
0
1
6
21
56
(x-3)*(x-2)*(x-1)*x*(x+1)/5!
5
5D volumes
0
0
0
0
0
0
1
7
28
(x-4)*(x-3)*(x-2)*(x-1)*x*(x+1)/6!
6
6D volumes
0
0
0
0
0
0
0
1
8
(x-5)*(x-4)*(x-3)*(x-2)*(x-1)*x*(x+1)/7!
7
7D volumes
0
0
0
0
0
0
0
0
1
(x-6)*(x-5)*(x-4)*(x-3)*(x-2)*(x-1)*x*(x+1)/8!

Formula

This formula is used to calculate each of the equations in the table: ∑(fv(t),t,1,x)→fv+1(x); f0(x)=x+1
This formula is used to find the value of any cell if given its x and y coordinates in the table: ∏(x-t,t=-1,y-1)/(y+1)! = x*(x+1)*(y-x)!*cos(180*y)/((x-y)*(-x!)*(y+1)*y!)
100*3!=600
Another pattern of the data is:
a
b
a+b

Useful Facts

Face-to-Face angle

If you form a triangle from points P(1/2,√(3)/6,√(6)/3) to Q(1/2,0,0) to R(1/2,√(3)/2,0) then the angles PQR=cos-1(1/3)≈70.5287793655° and QRP=RPQ=(180-cos-1(1/3))/2≈54.7356103172°.

Factorials by dividing Multi-dimensional volumes

Right tetrahedrons:
lim(∑((t/x)d,t-->1,x)/(f(x-1)*x),x-->infinity)→f(x)
0d: 1 * its point
1d: 1 * its length
2d: 1/2 its square
3d: 1/6 its cube
4d: 1/24 its tesseract
5d: 1/120 it 5d tesseract

Sliding

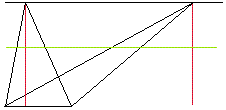Each of the two triangles share the same base. The red lines are the triangle's height; the heights are the same. The length of the green line is the same in each triangle. Therefore, the areas of both triangles is equal. .

Any tetrahedron:
Length of segment = base(point) * height/1
Area of triangle = base(length) * height/2
Volume of tetrahedron = base(area) * height/3
Volume of 4d tetrahedron = base(volume) * height/4
Volume of 5d tetrahedron = base(4d volume) * height/5

The equation for the volume of a tetrahedron (base * height / 3) is the same as for a pyramid and cone; this is because they each have an area base that go to a single point in the third dimension.

Triangulation

Each side of the triangle has a perpendicular line drawn. The point of intersection is where the center of the circle that has all three points of the triangle on it.
Top of Page

3D Octahedron

The octahedron has 1 volume, 8 areas, 12 lines, and 6 points. volume=edge_length3*sqrt(2)/6

The octohedron can be constructed by taking the center points of the faces of a cube. This method applies to multiple dimensions too.


Top of Page

3d dodecahedron

The icosahedron is related to the dodecahedron. They each have 30 segments and 1 3D volume. The icosahedron has 20 faces (2d areas) and 12 vertices (0d points), while the dodecahedron is the opposite, having 12 faces (2d areas) and 20 vertices (0d points). If you placed a point in the center of each area in one hedron, then took those points and connected them you would get the same shape of the other hedron.

dodecahedron

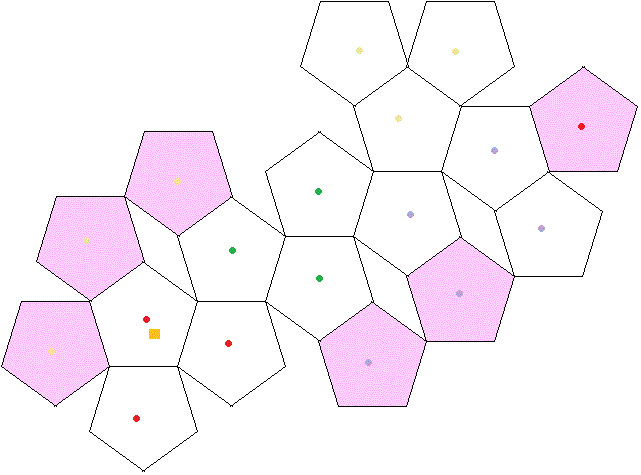
The colored dots in the picture are there to help you fold it into a dodecahedron. The shaded areas are areas that overlap. Cut out the object. After cutting, and creasing a fold on each line, glue the shape together.

The angle made from area to area is cos-1(-(√(5)+1)*√(2)/(2*√(9*√(5)+25))) ≈ 109.915883287°.

Lengths


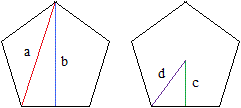
If each side of the pentagon is a length of 1 unit, then the lengths of the labled sides are written in the following table.
label
exact length
approximate length
a
(1+√(5))/2
1.61803398875
b
(√(5+√(5))+√(5-√(5)))*√(2)/4
1.53884176859
c
(1+√(5))*√(2)/(4*√(5-√(5)))
0.688190960236
d
√(2)/√(5-√(5))
0.850650808352

If each side of the pentagon is a length of (1+√(5))/2 units, then the lengths of the labled sides are written in the following table.
label
exact length
approximate length
a
(3+√(5))/2
2.61803398875
b
(1+√(5))*(√(5-√(5))+√(5+√(5)))*√(2)/8
2.48989828488
c
(3+√(5))*√(2)/(4*√(5-√(5)))
1.11351636441
d
(1+√(5))*√(2)/(2*√(5-√(5)))
1.37638192047

Coordinates

This table shows the coordinates of the dodecahedron which has 12 faces.
label
x
y
z
A
0
0
0
B
1
0
0
C
(√(5)+3)/4
√(2*(5+√(5)))/4
0
D
1/2
(√(5+√(5))+√(5-√(5)))*√(2)/4
0
E
(-√(5)+1)/4
√(2*(5+√(5)))/4
0
F
(1-√(5))/4
-√(2)/(2*√(5-√(5)))
√(10*(5+√(5)))/10
G
(√(5)+3)/4
-√(2)/(2*√(5-√(5)))
√(10*(5+√(5)))/10
H
(√(5)+5)/4
(3+√(5))*√(2)/(4*√(5-√(5)))
√(10*(5+√(5)))/10
I
1/2
(3+√(5)*3)*√(2)/(4*√(5-√(5)))
√(10*(5+√(5)))/10
J
-(√(5)+1)/4
(3+√(5))*√(2)/(4*√(5-√(5)))
√(10*(5+√(5)))/10
K
1/2
-(1+√(5))*√(2)/(4*√(5-√(5)))
(√(5-√(5))+√(5+√(5)))*√(10)/10
L
(√(5)+5)/4
(√(5)-1)*√(2)/(4*√(5-√(5)))
(√(5-√(5))+√(5+√(5)))*√(10)/10
M
(√(5)+3)/4
(2+√(5))*√(2)/(2*√(5-√(5)))
(√(5-√(5))+√(5+√(5)))*√(10)/10
N
(1-√(5))/4
(2+√(5))*√(2)/(2*√(5-√(5)))
(√(5-√(5))+√(5+√(5)))*√(10)/10
O
(-√(5)-1)/4
(√(5)-1)*√(2)/(4*√(5-√(5)))
(√(5-√(5))+√(5+√(5)))*√(10)/10
P
1/2
(√(5)-3)*√(2)/(4*√(5-√(5)))
(√(5-√(5))+2*√(5+√(5)))*√(10)/10
Q
(√(5)+3)/4
√(2)/(2*√(5-√(5)))
(√(5-√(5))+2*√(5+√(5)))*√(10)/10
R
1
√(2)/(2*√(5-√(5)))+√(5+√(5))*√(2)/4
(√(5-√(5))+2*√(5+√(5)))*√(10)/10
S
0
√(2)/(2*√(5-√(5)))+√(5+√(5))*√(2)/4
(√(5-√(5))+2*√(5+√(5)))*√(10)/10
T
(-√(5)+1)/4
√(2)/(2*√(5-√(5)))
(√(5-√(5))+2*√(5+√(5)))*√(10)/10
center
1/2
(1+√(5))*√(2)/(4*√(5-√(5)))
(√(5-√(5))+2*√(5+√(5)))*√(10)/20

Top of Page

3d icosohedron

icosahedron
A way to make the icosohedron is to glue slightly irregular 3D tetrahedrons together around a comman point, the center of the icosohedron.

The colored dots in the picture are there to help you fold it into an icosohedron. The shaded areas are areas that overlap. Cut out the object and cut the red lines. After cutting, and creasing a fold on each line, glue the shape together.

The angle made from area to area is cos-1(-√(5)/3) ≈ 138.189685104°.

Coordinates


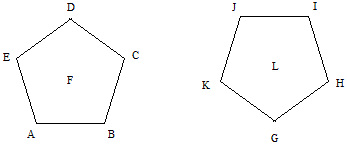
This table shows the coordinates of the upper (triagular) figure, which has 20 faces. These coordinates surround the center coodinate located at (1/2,√(3)/6,√(6)/3). The center of the 20 hedron is one unit away from each of its point.
label
x
y
z
A
0
0
0
B
1
0
0
C
(√(5)+3)/4
√(2*(5+√(5)))/4
0
D
1/2
(√(5+√(5))+√(5-√(5)))*√(2)/4
0
E
(-√(5)+1)/4
√(2*(5+√(5)))/4
0
F
1/2
(√(5)+1)*√(2)/(4*√(5-√(5)))
√(10*(5-√(5)))/10
G
1/2
(√(5)-3)*√(2)/(4*√(5-√(5)))
√(10*(5+√(5)))/10
H
(√(5)+3)/4
√(2)/(2*√(5-√(5)))
√(10*(5+√(5)))/10
I
1
√(2)/(2*√(5-√(5)))+√(5+√(5))*√(2)/4
√(10*(5+√(5)))/10
J
0
√(2)/(2*√(5-√(5)))+√(5+√(5))*√(2)/4
√(10*(5+√(5)))/10
K
(-√(5)+1)/4
√(2)/(2*√(5-√(5)))
√(10*(5+√(5)))/10
L
1/2
(√(5)+1)*√(2)/(4*√(5-√(5)))
(√(5-√(5))+√(5+√(5)))*√(10)/10
center
1/2
(√(5)+1)*√(2)/(4*√(5-√(5)))
√(10*(5+√(5)))/20

Top of Page

3d Hexagon Equivalent

This section made a false assumption; circles can be tightly stacked in two dimensions, but it is impossible for there to be tightly stack spheres in 3 dimensions with all of the spheres of the same size.

This table shows the coordinates, like the icosahedron, but a problem occurred because of the false assumption; there is a small gap between the first and last points which should be the same point. These coordinates surroud the center coodinate located at (1/2,√(3)/6,√(6)/3). The center of this imaginary hedron is one unit away from each of its points.

label
x
y
z
a
A
1/2
√(3)/2
0
0
B
0
0
0
0
C
1
0
0
0
D
4/3
√(3)*4/9
√(6)*2/9
0
E
4/9
√(3)*20/27
√(6)*10/27
0
F
-1/3
√(3)*4/9
√(6)*2/9
0
G
0
H
0
I
0
J
0
K
0
L
0
M
0
N
0
O
0
P
0
Q
0
R
0
S
0
T
0
U
1/2
√(3)/6
√(6)/12
√(10)/4
V
W
X
Y
Z


This table shows coordinates, like the dodecahedron.
label
x
y
z
a
A
1/2
√(3)/6
√(6)/12
0
B
5/6
√(3)*5/18
√(6)*5/36
0
C
13/18
√(3)*25/54
√(6)*25/108
0
D
5/18
√(3)*25/54
√(6)*25/108
0
E
1/6
√(3)*5/18
√(6)*5/36
0
F
0
G
0
H
0
I
0
J
0
K
0
L
0
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z

data *with false assumption*

This table shows the number of lines, areas, volumes, four dimensional volumes, ... in the point-to-line-to-hexagon-to-20 hedron-to- pattern.
Dimensions
0
1
2
3
4
5
6
7
x
Points
1
2
6
12
x*(x+1)
Lines
0
1
6
30
96
Areas
0
0
1
20
130
548
Volumes
0
0
0
1
62
4D volumes
0
0
0
0
1
5D volumes
0
0
0
0
0
1
6D volumes
0
0
0
0
0
0
1
7D volumes
0
0
0
0
0
0
0
1

This formula is used to calculate each of the equations in the table: ∑(fv(t),t,1,x)→fv+1(x); f0(x)=x*(x+1)
Another pattern of the data is:
a
b
3a+2b

Top of Page

Sphere

Every sphere has an infinate number of points at the same distance from a particular point (the center of the sphere. The equation of a 3D sphere with its epicenter at (0,0,0) is √(x2+y2+z2) = length_of_radius. A pattern for making spheres in multiple dimensions is:

0D: a point
1D: a line
2D: a line with a smeared rotation into the 2nd dimension.
3D: a circle with a smeared rotation into the 3rd dimension.
4D: a sphere with a smeared rotation into the 4th dimension.
5D: a 4D sphere with a smeared rotation into the 5th dimension.
6D: a 5D sphere with a smeared rotation into the 6th dimension.
# of Dimensions
circumference, surface area, ...
area, volume, ...
0
0
1
1
2
2*r
2
r*π*2
r2*π
3
r2*π*4
r3*π*4/3
4
r3*π2*2
r4*π2/2
5
r4*π2*8/3
r5*π2*8/15
6
r5*π3
r6*π3/6
7
r6*π3*16/15
r7*π3*16/105
8
r7*π4/3
r8*π4/24
9
r8*π4*32/105
r9*π4*32/945
10
r9*π5/12
r10*π5/120

Top of Page

Comments

How do you think this webpage or website should be updated, in terms of either content, appearance, or other? Your comments are appreciated!
If you disagree with something, think something needs to be clarified, want more information on something, find a mistake somewhere, or find a problem with the function of something on this website, please let me know by leaving a comment below.

Username:
Comment:

Comment will be viewable to:
Public: anyone accessing this website.
Private: only the author of this website.

CAPTCHA
Enter the numbers from the CAPTCHA image:

Posted By: buy pletal     Page Posted: Home Page/Mathematics Portal/Multiple Dimensions     Time/Date Posted: 2023-12-08-08-20-29     Length of Message: 258
Fantastic content, Kudos. buy pletal online Passion the site-- extremely individual friendly and lots to see! buy pletal Wonderful images, the color and depth of the images are breath-taking, they draw you in as though you are a part of the make-up.

Posted By: toinkvott     Page Posted: Home Page/Mathematics Portal/Multiple Dimensions     Time/Date Posted: 2022-06-08-00-51-08     Length of Message: 312
https://newfasttadalafil.com/ - cialis and viagra sales Bvqfqk buy cialis generic online cheap Brmyve fetus for removal of uid and cells for a pregnant woman so that the karyotype of the baby can be examined. Xevcif https://newfasttadalafil.com/ - how much does cialis cost Yfpzwm Propecia Side Effects Temporary

Posted By: RbyDT     Page Posted: Home Page/Mathematics Portal/Multiple Dimensions     Time/Date Posted: 2021-12-03-20-01-08     Length of Message: 22
buy doxycycline online

Posted By: iesahequxexo     Page Posted: Home Page/Mathematics Portal/Multiple Dimensions     Time/Date Posted: 2021-01-15-06-15-09     Length of Message: 145
http://mewkid.net/when-is-xuxlya2/ - Amoxicillin 500mg Amoxicillin Online vet.zpia.floydsphilosophy.com.dsq.vy http://mewkid.net/when-is-xuxlya2/

Posted By: ugeitaixuxueh     Page Posted: Home Page/Mathematics Portal/Multiple Dimensions     Time/Date Posted: 2021-01-15-05-45-11     Length of Message: 143
http://mewkid.net/when-is-xuxlya2/ - Buy Amoxicillin Online Amoxicillin afe.shba.floydsphilosophy.com.ggb.af http://mewkid.net/when-is-xuxlya2/

Posted By: ramboTouff     Page Posted: Home Page/Mathematics Portal/Multiple Dimensions     Time/Date Posted: 2020-11-04-03-56-26     Length of Message: 209
What have you been up to? I am fascinated about covid19. Can you talk about it? If the same thread is opened please redirect my post :). Thanks :). PS: I don't know any people with covid and you? rambo :D

Posted By: ramboTouff     Page Posted: Home Page/Mathematics Portal/Multiple Dimensions     Time/Date Posted: 2020-10-31-15-15-45     Length of Message: 209
What have you been up to? I am fascinated about covid19. Can you talk about it? If the same thread is opened please redirect my post :). Thanks :). PS: I don't know any people with covid and you? rambo :D

Posted By: DalanoTort     Page Posted: Home Page/Mathematics Portal/Multiple Dimensions     Time/Date Posted: 2019-12-19-07-37-29     Length of Message: 147
Vaginitis with vaginal discharge is a common problem, causing 10 million women each year to visit a physicians office for care. yeast infection